Steps in Calculating Internal Rate of Return (IRR)
Launching and growing a business is important for startups, entrepreneurs, and early-stage investors. Knowing how to measure the success and profitability of their ventures is essential. A financial metric that provides practical insights into evaluating the efficiency and growth potential of investments is the consideration of the timing and magnitude of cash flows over time.
By mastering IRR, founders and investors can better assess which opportunities are likely to generate the best returns and make more informed strategic decisions that drive sustainable growth.

What is the Internal Rate of Return (IRR)?
IRR is one of the capital investment evaluation techniques used by investors while making investment decisions. IRR is the discount rate that makes the net present value (NPV) of cash flows from a particular project or investment equal to zero.
Calculating IRR helps assess the profitability of potential investments and is commonly used in capital budgeting and investment analysis.
Uses of IRR
The internal rate of return makes the project attractive since the cash outflows and the present value of the inflows are equal. The uses of this rate are enumerated as follows:
- The IRR acts as the effective interest rate for savings and loan calculations.
- The profitability, effectiveness, quality, or yield of an investment is indicated by the internal rate of return.
- An investment should only be made if its profitability, as determined by the internal rate of return, is higher than a minimum acceptable rate of return to maximize the value of a corporation. Hence this rate is a crucial factor in investment decisions.
- Businesses utilize IRR in capital budgeting to contrast the profitability of various capital projects.
- From the limited partners’ perspective, IRR is also utilized in private equity as a way to gauge how well the general partner is managing investments.
How to Calculate IRR?
The IRR is the estimated interest rate at which the initial capital investment must have increased to achieve the ending value from the beginning value, given a specified range of dates. It is calculated by dividing the future value by the present value of an investment.
Steps in calculating IRR
The method for calculating IRR varies depending on the pattern of net cash flows over an investment’s useful life. The steps for manually calculating the IRR metric are as follows.
1. Gather Cash Flow Data
List all expected cash flows from the investment, including the initial outlay (usually a negative value) and all future inflows and outflows, period by period (e.g., yearly).
2. Set Up the IRR Equation
The IRR is the rate r that satisfies the following equation:
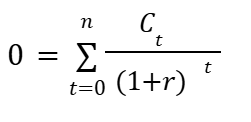
Where:
- Ct = cash flow at time t
- r = IRR
- t = time period
3. Estimate Discount Rates
Choose two discount rates as initial guesses – one that results in a positive NPV and another that results in a negative NPV.
4. Calculate NPVs for Each Rate
Compute the NPV of the cash flows at each chosen discount rate.
5. Interpolate to Find IRR
Use linear interpolation to estimate the IRR:
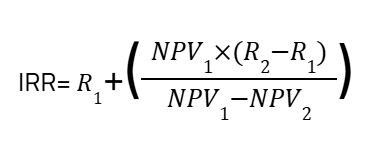
Where:
- R1 = lower discount rate
- R2 = higher discount rate
- NPV1 = NPV at R1
- NPV2 = NPV at R2
6. Refine the Estimate (If Needed)
If the result is not sufficiently close to zero, repeat the process with new rates until the NPV approaches zero.
7. Use Financial Tools for Efficiency
Because the IRR equation cannot be solved algebraically for most real-world cash flow series, use financial calculators or spreadsheet software (like Excel’s IRR or XIRR functions) for more complex or irregular cash flows.
Key Points
- IRR is found where the NPV of cash flows equals zero.
- The process is iterative and often requires trial and error or interpolation.
- Financial calculators and spreadsheet functions greatly simplify the process for real-world applications.
Example for Calculating IRR
An investor is considering a project that requires an initial investment of $10,000. The project is expected to generate net cash inflows over the next 4 years of the amounts 2,000, 3,000, 4,000 and 4,000 for each year respectively.
We want to calculate the IRR manually using interpolation.
Steps 1 and 2: List the Cash Flows and Set up the IRR equation
| Year | Cash Flow |
| 0 | -10,000 |
| 1 | 2,000 |
| 2 | 3,000 |
| 3 | 4,000 |
| 4 | 4,000 |
IRR equation:

Step 3: Choose Discount Rates
- Lower Rate: 8%
- Higher Rate: 12%
Step 4: Calculate NPV at Each Discount Rate
NPV at 8%:
| Year | Cash Flow ($) | Discount Factor @ 8% | Present Value ($) |
|---|---|---|---|
| 0 | -10,000 | 1 | -10,000 |
| 1 | 2,000 | 0.9259 | 1,852 |
| 2 | 3,000 | 0.8573 | 2,572 |
| 3 | 4,000 | 0.7938 | 3,175 |
| 4 | 4,000 | 0.735 | 2,940 |
| NPV | 539 |
NPV at 12%:
| Year | Cash Flow ($) | Discount Factor @ 12% | Present Value ($) |
|---|---|---|---|
| 0 | -10,000 | 1 | -10,000 |
| 1 | 2,000 | 0.8929 | 1,786 |
| 2 | 3,000 | 0.7972 | 2,392 |
| 3 | 4,000 | 0.7118 | 2,847 |
| 4 | 4,000 | 0.6355 | 2,542 |
| NPV | -433 |
Step 5: Apply Interpolation Formula
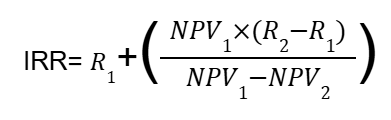
IRR = 8 + ((539 / (539 -(-433))) × (12−8)
= 8 + 0.55 x (4)
= 10.2%
Check the NPV at 10.2%:
| Year | Cash Flow ($) | Discount Factor @ 10.2% | Present Value ($) |
|---|---|---|---|
| 0 | -10,000 | 1 | -10,000.00 |
| 1 | 2,000 | 0.9074 | 1,814.80 |
| 2 | 3,000 | 0.8234 | 2,470.20 |
| 3 | 4,000 | 0.7472 | 2,988.80 |
| 4 | 4,000 | 0.6781 | 2,712.40 |
| NPV | -13.8 |
At 10.2%, the NPV is approximately -$13.80, which is very close to zero
Step 6: Refine the Estimate
Check NPV at 10.14%:
| Year | Cash Flow ($) | Discount Factor @ 10.14% | Present Value ($) |
|---|---|---|---|
| 0 | -10,000 | 1 | -10,000.00 |
| 1 | 2,000 | 0.9079 | 1,815.80 |
| 2 | 3,000 | 0.8243 | 2,472.90 |
| 3 | 4,000 | 0.7485 | 2,994.00 |
| 4 | 4,000 | 0.6795 | 2,718.00 |
| NPV | 0.7 |
The NPV at 10.14% is 0.7 (almost equal to 0), this means that the IRR is at 10.14%.
What is Good IRR?
A good IRR is one that exceeds your required rate of return and is competitive within your industry and risk profile. Higher IRRs generally indicate higher risk, so context and comparison to alternatives are essential.
Summary Table: Typical “Good” IRR Ranges
| Investment Type | Typical "Good" IRR Range |
|---|---|
| Low-risk (bonds, annuities) | 5-10% |
| Moderate-risk | 10-15% |
| High-risk (VC, startups) | 20-30%+ |
| Real estate (conservative) | 8-12% |
| Real estate (moderate) | 15-20% |
| Real estate (high-risk) | 20%+ |
Common Pitfalls When Calculating IRR Manually or With Software
By understanding and addressing the pitfalls, you can ensure more accurate and reliable IRR calculations for investment analysis.
- Cash Flow Timing Errors: Misaligning cash flows with their correct periods (e.g., recording a Year 2 inflow in Year 3) leads to inaccurate IRR results. This is a frequent manual error and can also occur if dates are entered incorrectly into software.
- Inconsistent Cash Flow Intervals: Mixing periods (e.g., combining monthly and annual cash flows) without standardization skews IRR calculations. Always use uniform intervals throughout the analysis.
- Inaccurate Cash Flow Projections: Over- or underestimating the amount or timing of cash flows distorts the IRR, making investments appear more or less attractive than reality.
- Multiple IRRs: Projects with non-conventional cash flows (where cash flows change sign more than once) can result in multiple IRRs. Most software, including Excel, only displays the first IRR it finds, which may not be the relevant one for decision-making.
- No IRR Exists: If all cash flows are positive or all are negative, the IRR calculation will fail (e.g., Excel returns #NUM!). Minimum of one negative and one positive cash flow are required for a valid IRR.
- Overlooking Reinvestment Rate Assumptions: IRR assumes that cash flows are reinvested at the IRR itself, which is often unrealistic and leads to overestimated returns. The Modified IRR (MIRR) can address this by allowing for more realistic reinvestment rates.
- Manual Calculation Complexity: Solving the IRR equation manually is iterative and error-prone, especially for complex or irregular cash flows. Manual errors are common, particularly when you prefer manual calculations for investment analysis.
- Software-Specific Issues: Excel and similar tools may return false IRRs, fail to converge (after too many iterations), or misinterpret cash flow patterns. Using the “guess” parameter or switching to MIRR can help, but vigilance is required.
- Ignoring Project Size: IRR does not account for the exact size of the investment, so two projects with vastly different scales can have identical IRRs but very different financial impacts.
Get a business valuation from Eqvista!
When there are many investment alternatives, the Internal Rate of Return is appropriate. This facilitates decision-making by allowing investors to rate their investment options from highest to lowest IRR. To make decisions regarding investments, the valuation of the business is crucial.
Need help with your business valuation? Eqvista aids you with business valuation and filing. Feel free to contact us anytime!
